意見や質問，訂正依頼等は
のいずれかまでお願いします．
まず剰余群とは何かについて考えましょう．剰余群とは，群 G の正規部分群 N⊲G があったときに G を N で割ったもの G/N ですが，上で注意したように，ある群準同型 φ:G→H があって N=Ker(φ) なので（例えば H=G/N として，φ=π:G↠G/N を標準的な全射とすればよいです），初めから G/Ker(φ) というものを考えることにします．この Coim(φ):=G/Ker(φ) を φ の余像（coimage）といいます．
では Coim(φ) とは何でしょうか．G の異なる元 g,h∈G が φ(g)=φ(h) であるとき，これらの元を「φ 無駄」（数学用語ではありません）と呼ぶことにすれば，Ker(φ) は G の φ 無駄を集めてきたものなので，Coim(φ) は「G の φ 無駄を過不足なく潰したもの」となります．（そもそも剰余群 ≒ 商集合とはそういうものでした．）
従って φ 無駄の無い Coim(φ) は Im(φ) と同一視できると期待できますが，実際にそうだというのが（第一）準同型定理の主張です．
ではこの「φ 無駄の無さ」を圏論的にどう表現すればよいのでしょうか．Ker(φ) の場合に倣って，群 Coim(φ) と群準同型 π:G↠Coim(φ) のペアとして考えていきましょう．Coim(φ) について今知っていることは，
ことです．
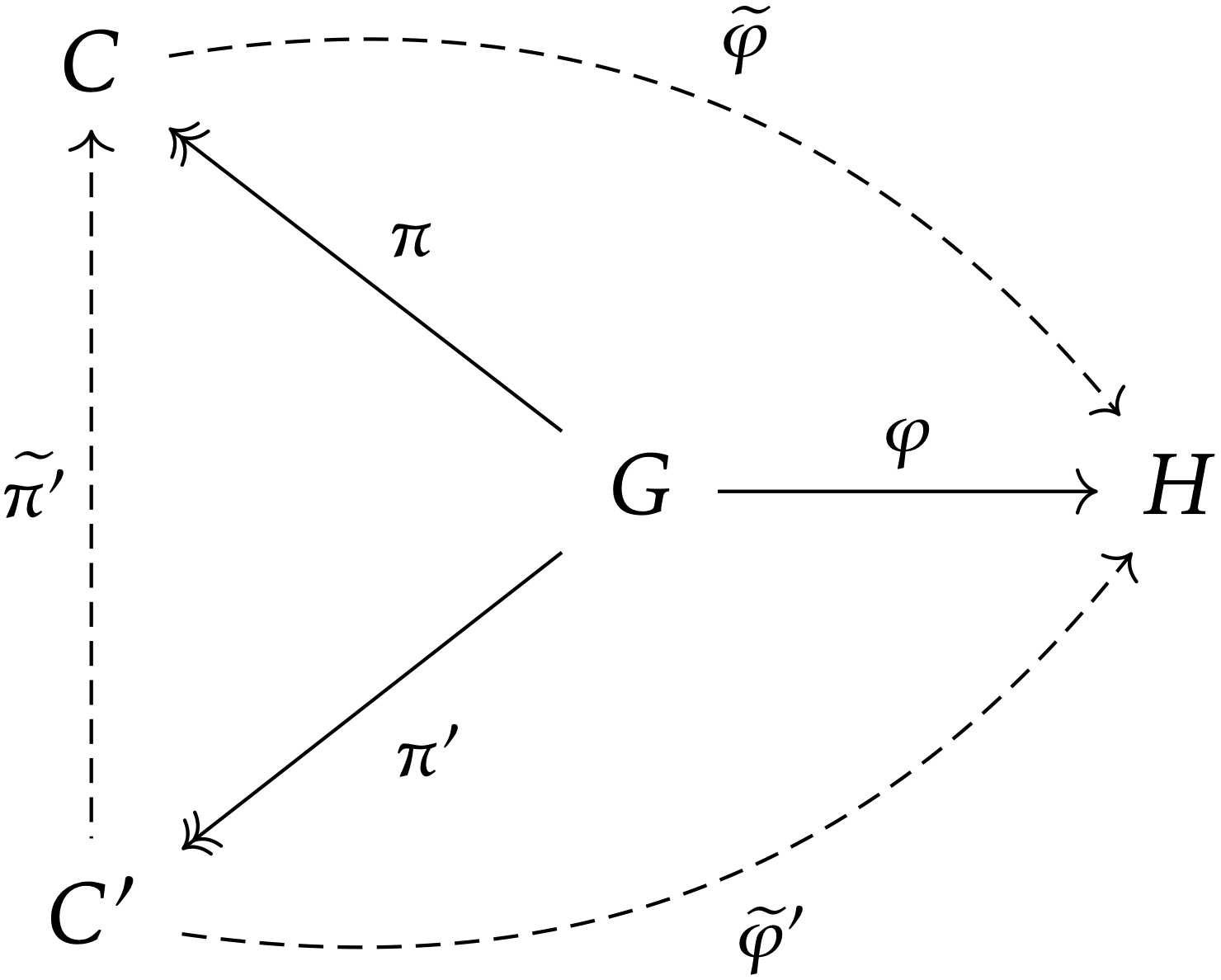
そこで，別の群 C′ と群準同型 π′:G→C′ のペアであって，
であるとしましょう．核との類推によると，ただ一つの群準同型 ~π′:C′→Coim(φ) が存在して，π=~π′∘π′ かつ ˜φ′=˜φ∘~π′ となると予想できます．
この群準同型 ~π′:C′→C を構成するために，まず Ker(π′)⊂Ker(φ) に注意しましょう．すると，群準同型 π0:G/Ker(π′)→G/Ker(φ)=Coim(φ) が π0(gKer(π′)):=gKer(φ) によって well-defined に定まります．さらに準同型定理によって群同型 π1:C′→G/Ker(π′) が存在するので， ~π′:=π0∘π1 とおけば，必要な条件をすべて満たすことが分かります．従って次の余像の普遍性（universal property of coimages）を得ます：
群の間の群準同型 φ:G→H が与えられたとき，次の条件を満たす群 C と全射群準同型 π:G→C のペアが同型を除いて一意に存在する：
次に，全射を圏論的に書き換えましょう．写像 φ:X→Y が全射（surjection）であるとは， ∀y∈Y, ∃x∈X, y=φ(x) となることです．一方，圏論では次のような定義があります：
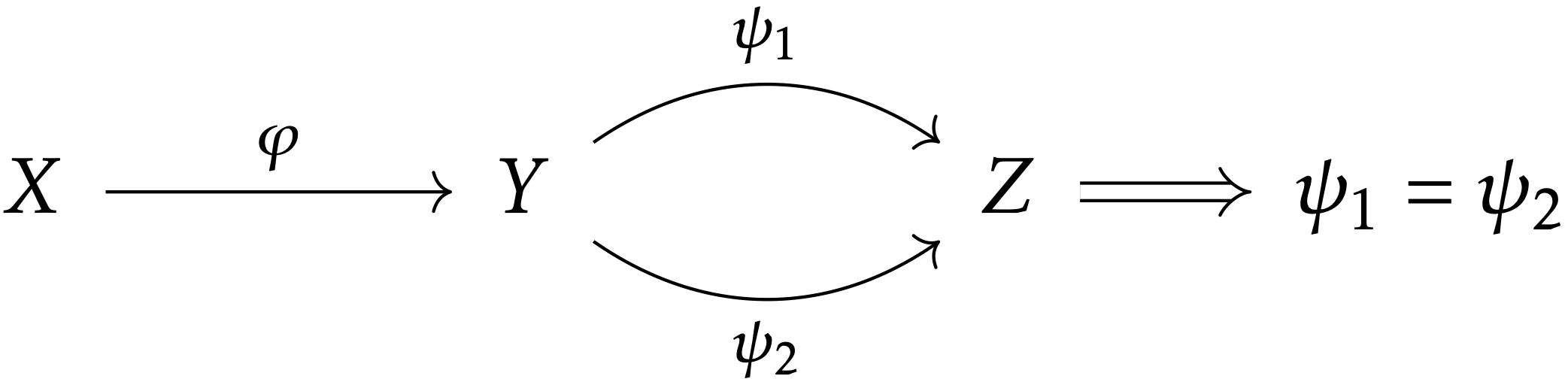
写像 φ:X→Y がエピ射（epimorphism）であるとは，任意の写像 ψ1,ψ2:Y→Z に対して，ψ1∘φ=ψ2∘φ ならば ψ1=ψ2 なることをいう． ∀ψ1,ψ2:Y→Z, ψ1∘φ=ψ2∘φ⟹ψ1=ψ2
一般にこれらは一致しませんが，集合の圏等の特別な場合には一致します．群の圏もその一つです．すなわち，
群準同型 φ:G→H に対して，φ が全射であるための必要十分条件は φ がエピ射であることである． φ:surj.⟺φ:epi.
⟹)
φ を全射とし，ψ1∘φ=ψ2∘φ なる任意の群準同型 ψ1,ψ2:H→H′ を取る．φ の全射性より，φ∘ψ=idH なる写像 ψ:H→G が存在するから， ψ1=ψ1∘(φ∘ψ)=(ψ1∘φ)∘ψ=(ψ2∘φ)∘ψ=ψ2∘(φ∘ψ)=ψ2 となる．よって，φ はエピ射．
⟸)
φ をエピ射とし，次のような群準同型 ψ1,ψ2:H→H/Im(φ) を考える： ψ1(h):=hIm(φ),ψ2(h):=Im(φ). 容易に分かるように ψ1∘φ=ψ2∘φ だから，φ のエピ性より，ψ1=ψ2．よって φ は全射となる．
この証明に出てきた Coker(φ):=H/Im(φ) は余核（cokernel）と呼ばれ，核と圏論的に双対的な概念です．
もちろん上の証明では，次のよく知られた事実を用いました：
集合間の写像 φ:X→Y が全射であるための必要十分条件は，ある写像 ψ:Y→X が存在して，φ∘ψ=idY とできることである．
写像 φ:X→Y が単射であるための必要十分条件は，ある写像 ψ:Y→X が存在して，ψ∘φ=idX とできることである．
群準同型 φ:G→H が全射であるための必要十分条件は，余核が Coker(φ)={1:=Im(φ)} となることである．
群準同型 φ:G→H が単射であるための必要十分条件は，核が Ker(φ)={1} となることである．
ついでなので単射についても見てみましょう．写像 φ:X→Y が単射（injection）であるとは， ∀x1,x2∈X, x1≠x2⟹φ(x1)≠φ(x2) となることです．圏論では，
写像 φ:X→Y がモノ射（monomorphism）であるとは，任意の写像 ψ1,ψ2:Z→X に対して，φ∘ψ1=φ∘ψ2 ならば ψ1=ψ2 なることをいう． ∀ψ1,ψ2:Z→X, φ∘ψ1=φ∘ψ2⟹ψ1=ψ2
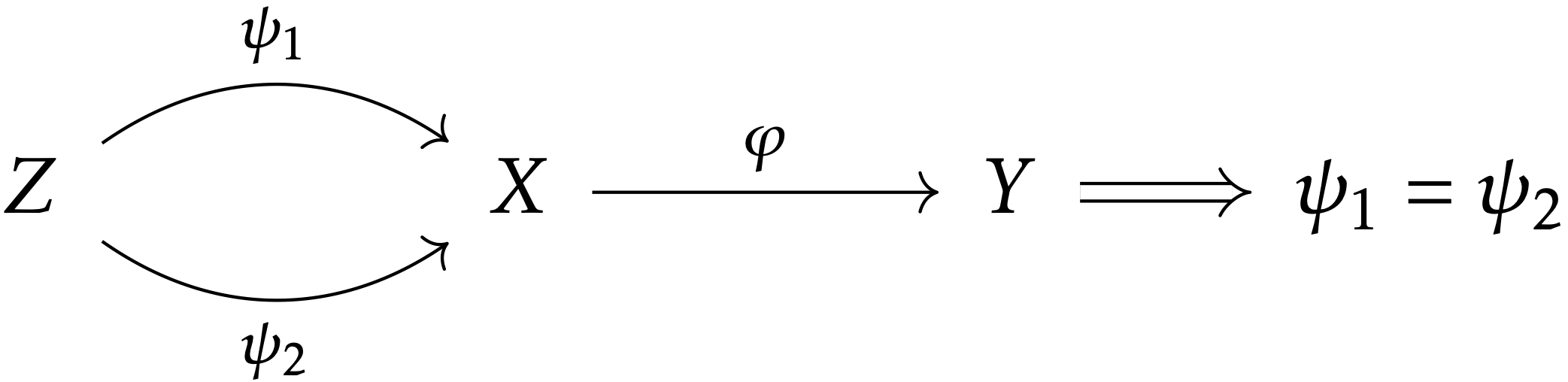
これらも一般には一致しませんが，集合の圏や群の圏では一致します．
群準同型 φ:G→H に対して，φ が単射であるための必要十分条件は φ がモノ射であることである． φ:inj.⟺φ:mono.
⟹)
φ を単射とし，φ∘ψ1=φ∘ψ2 なる任意の群準同型 ψ1,ψ2:H′→H を取る．φ の単射性より，ψ∘φ=idG なる写像 ψ:H→G が存在するから， ψ1=(ψ∘φ)∘ψ1=ψ∘(φ∘ψ1)=ψ∘(φ∘ψ2)=(ψ∘φ)∘ψ2=ψ2 となる．よって，φ はモノ射．
⟸)
φ をモノ射とし，次のような群準同型 ψ1,ψ2:Ker(φ)→G を考える： ψ1(g):=g,ψ2(g):=1. 容易に分かるように φ∘ψ1=φ∘ψ2 だから，φ のモノ性より，ψ1=ψ2．よって φ は単射．
直積の普遍性は，大雑把に言って，「ペアを作ること」です．群 G1,G2 とそれらの元 g1∈G1,g2∈G2 があったときに，ペア (g1,g2)∈G1×G2 を作ることができます．また，群準同型 φ1:H→G1,φ2:H→G2 があったときに，ペア (φ1,φ2):H→G1×G2 を， (φ1,φ2)(h):=(φ1(h),φ2(h)) によって定めることができます．さらに，群準同型 φ1:G1→H1 と φ2:G2→H2 から，(φ1×φ2)(g1,g2):=(φ1(g1),φ2(g2)) という新たな群準同型 φ1×φ2:G1×G2→H1×H2 が構成されます． このことをまとめると，
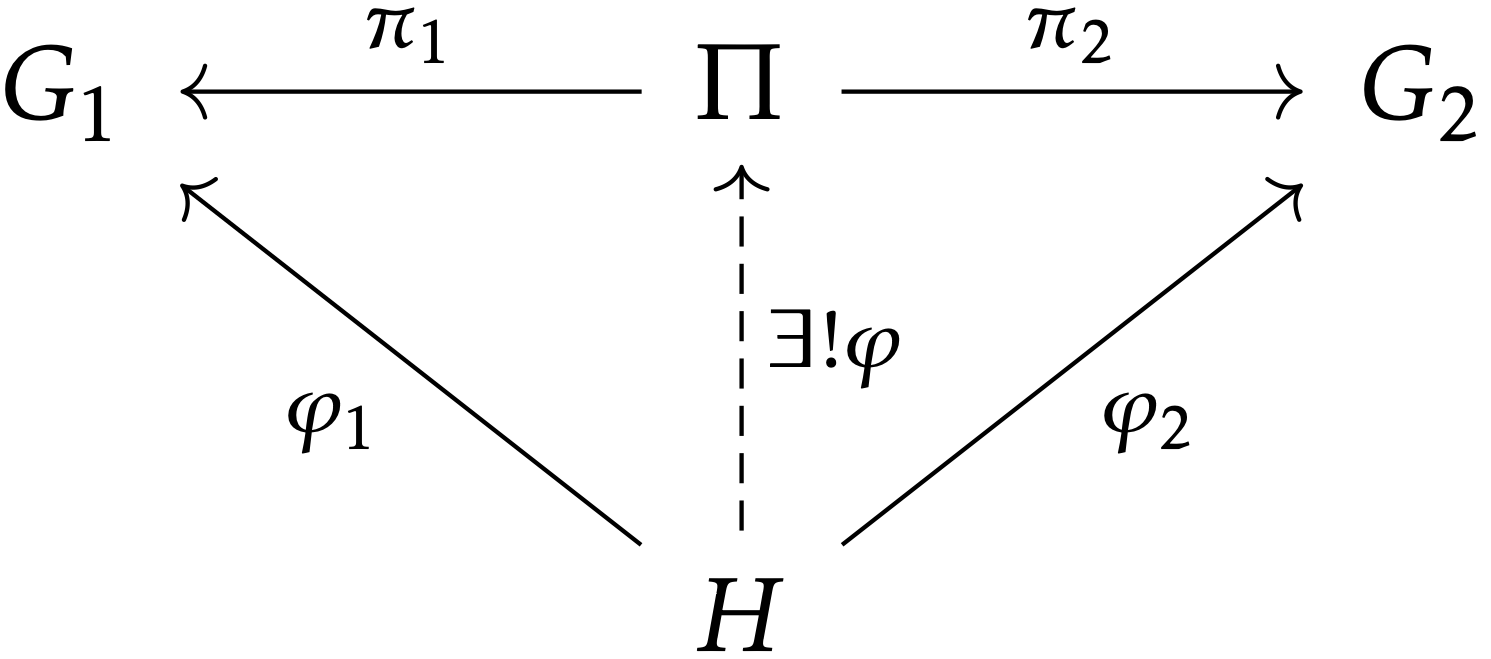
群 G1,G2 に対して，次の条件を満たす群 Π と群準同型 π1:Π→G1,π2:Π→G2 が同型を除いて一意に存在する：
もちろん，Π=G1×G2 で，π1,π2 は標準的な射影，φ=(φ1,φ2) です．
G1,G2,H1,H2 という群と群準同型 φ1:G1→H1，φ2:G2→H2 を取る．π1:G1×G2↠G1,π2:G1×G2↠G2,π′1:H1×H2↠H1,π′2:H1×H2↠H2 を標準的な射影とする．このとき，ただ一つの群準同型 φ:G1×G2→H1×H2 が存在して， φ1∘π1=π′1∘φ,φ2∘π2=π′2∘φ となる．
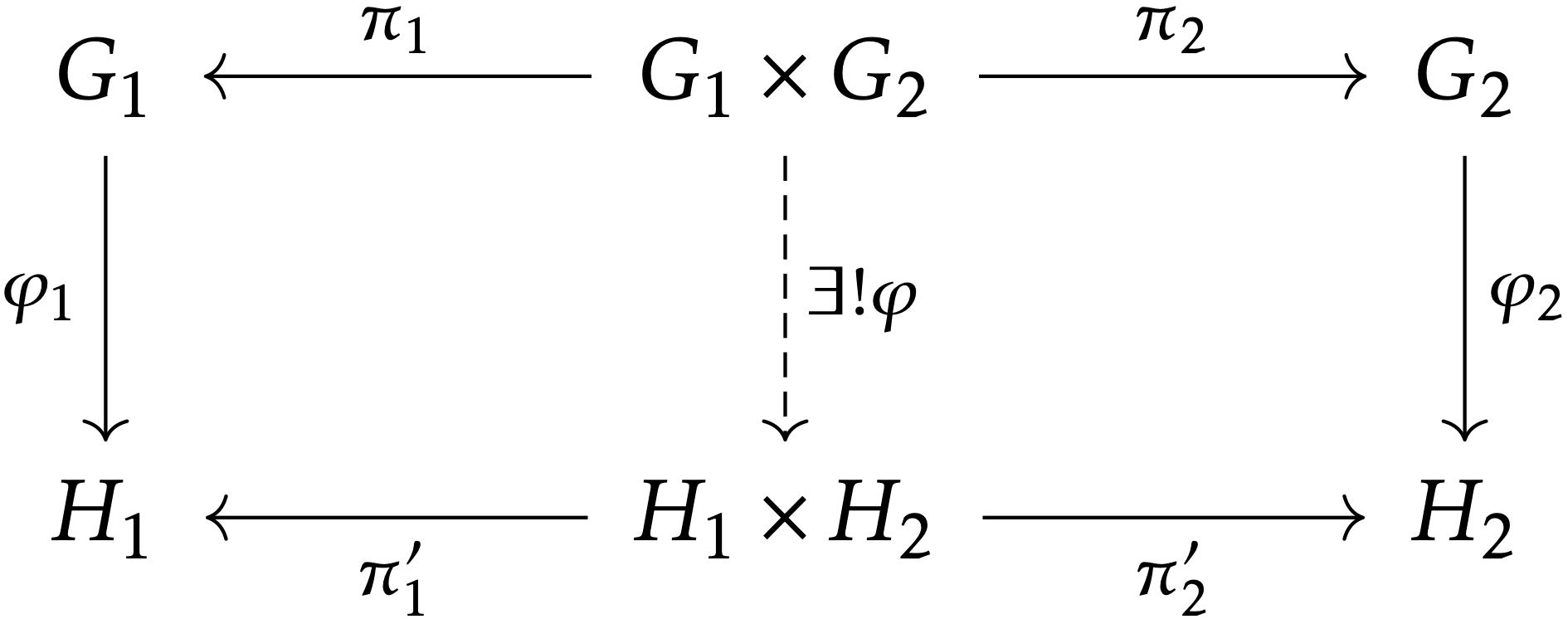
φ=φ1×φ2:=(φ1∘π1,φ2∘π2) である．
直和の普遍性は，「包含すること」です．「埋め込み」と言ってもいいです．群 G1 と G2 があったときに，これらを部分群として含むような最小の群が直和 G1⊕G2 です．G1 と G2 は標準的な入射によって，自然に G1⊕G2 の部分群とみなすことができます．さらに，群準同型 φ1:G1→H,φ2:G2→H があれば，それらを拡張した群準同型 ⟨φ1,φ2⟩:G1⊕G2→H が存在します．具体的には， ⟨φ1,φ2⟩(⋯gnhngn+1hn+1⋯)=⋯φ1(gn)φ2(hn)φ1(gn+1)φ2(hn+1)⋯ というように定義されます（gn∈G1,hn∈G2）．直積のときと同じように，群準同型 φ1:G1→H1 と φ2:G2→H2 を考えましょう．写像 φ1⊕φ2:G1⊕G2→H1⊕H2 を， φ1⊕φ2:=⟨ι′1∘φ1,ι′2∘φ2⟩ （ι′1:H1↪H1⊕H2,ι2:H2↪H1⊕H2 は標準的な入射）によって定めれば，これは群準同型になります．まとめると，
群 G1,G2 に対して，次の条件を満たす群 Σ と群準同型 ι1:G1→Σ,ι2:G2→Σ が同型を除いて一意に存在する：
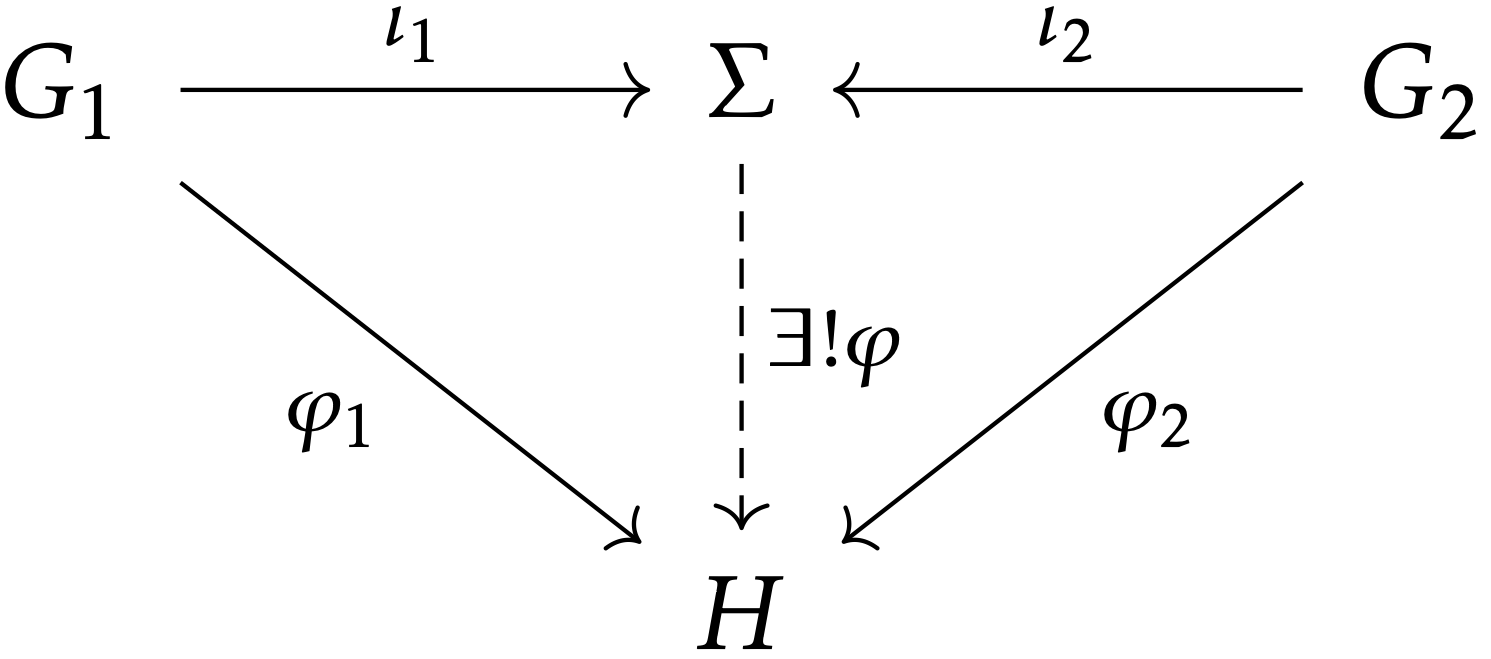
この場合は Σ=G1⊕G2 で，ι1,ι2 は標準的な入射，φ=⟨φ1,φ2⟩ です．
G1,G2,H1,H2 という群と群準同型 φ1:G1→H1，φ2:G2→H2 を取る．ι1:G1↪G1⊕G2,ι2:G2↪G1⊕G2,ι′1:H1↪H1⊕H2,ι′2:H2↪H1⊕H2 を標準的な入射とする．このとき，ただ一つの群準同型 φ:G1⊕G2→H1⊕H2 が存在して， φ∘ι1=ι′1∘φ1,φ∘ι2=ι′2∘φ2 となる．
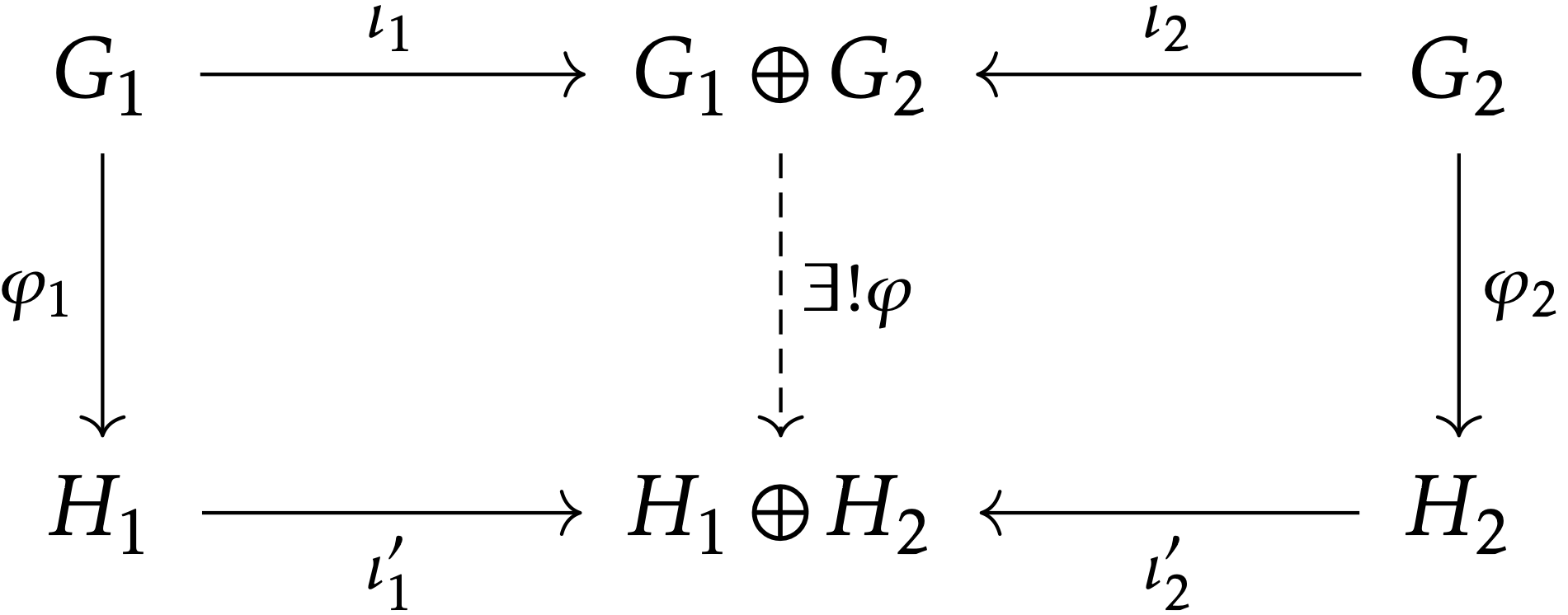
φ=φ1⊕φ2:=⟨ι′1∘φ1,ι′2∘φ2⟩ である．
Abel 化の普遍性は，その名の通り「可換性」でしょう．群 G とそのAbel 化 AbG，および標準的な全射 π:G↠AbG を考えます．
可換群 H と群準同型 φ:G→H があれば，任意の g1,g2∈G に対して φ(g1g2)=φ(g1)φ(g2)=φ(g2)φ(g1)=φ(g2g1) が成り立つので，[g1,g2]:=g1g2g−11g−12∈Ker(φ) となります．よって Ker(π)=[G,G]⊂Ker(φ) が分かります．すると，群準同型 ˜φ:AbG→H が， ˜φ(g[G,G]):=φ(g) によって well-defined に定まります．この ˜φ は，当然 ˜φ∘π=φ を満たします．
群 G に対して，次の条件を満たす群 A と群準同型 π:G→A とペアが同型を除いて一意に存在する：
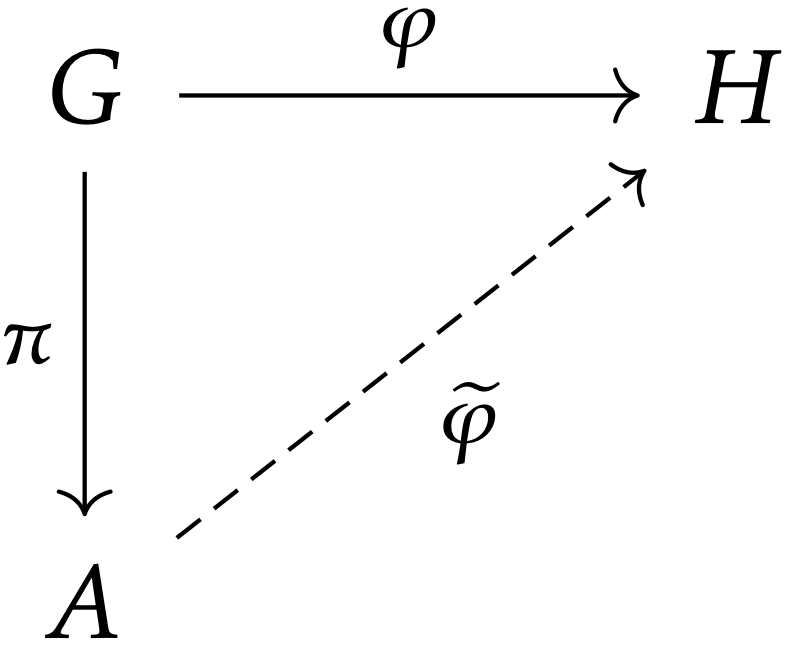
群 G,H と群準同型 φ:G→H を任意に取る．π:G↠AbG,π′:H↠AbH を標準的な全射とする．このとき，ただ一つの群準同型 ˜φ:AbG→AbH が存在して， ˜φ∘π=π′∘φ となる．
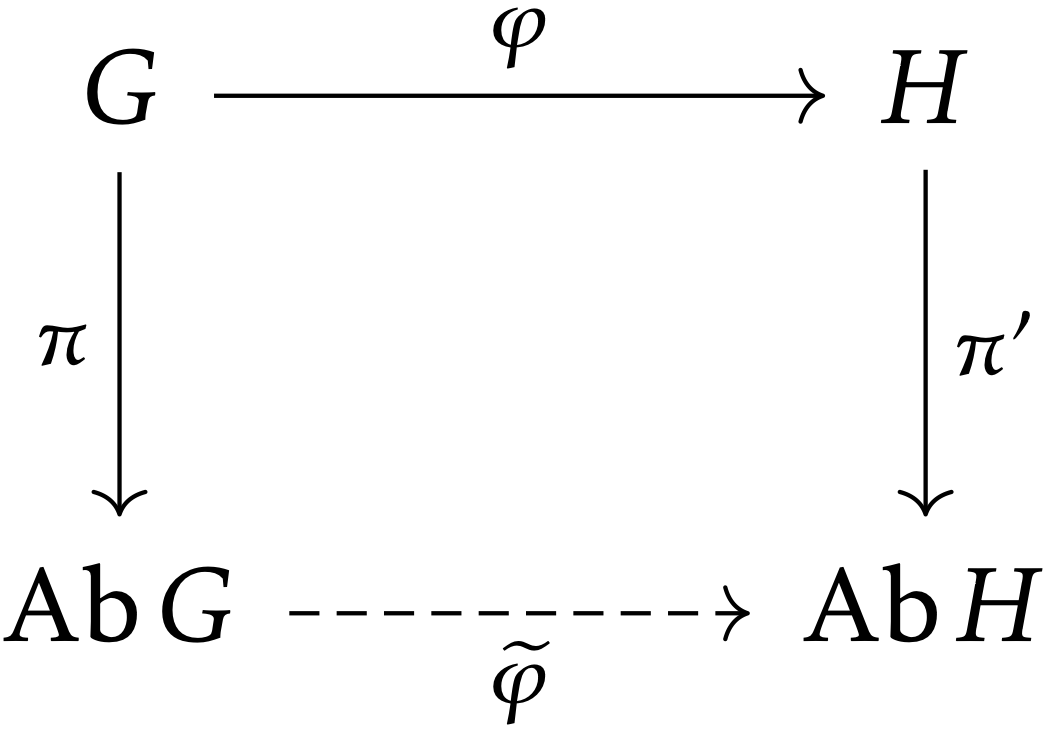
可換群 AbH と群準同型 π′∘φ:G→AbH に対して Abel 化の普遍性を適用すればよい．
圏論を学んでいる人なら，上の三つ（直積，直和，Abel 化）が関手であることに気づくでしょう．（実は核や余像も関手ですが，ここでは省略します．）つまり，直積と直和は ×,⊕:Grp×Grp→Grp という関手，Abel 化は Ab:Grp→Abl という関手になっています．ここで，Grp は群とその間の群準同型からなる圏であり，Abl は可換群とその間の群準同型からなる圏です．
さらに，Theorems によると，次のような（集合としての）全単射があります： Grp(H,G1×G2)≅Grp(H,G1)×Grp(H,G2),φ↦(π1∘φ,π2∘φ),Grp(G1⊕G2,H)≅Grp(G1,H)×Grp(G2,H),φ↦(φ∘ι1,φ∘ι2),Abl(G,A)≅Grp(AbG,A),φ↦φ∘π. ここで，G,G1,G2,H は群，A は可換群，π,π1,π2,ι1,ι2 は標準的な群準同型です． 実は，これらの全単射は自然同型（natural isomorphism）です．その意味は，上の全単射を関手間の変換（の G1,G2,H, etc. における対応）と見たときに，これらが自然変換である，ということです．それは，Theorems の「ただ一つの」という部分を使えば示すことができます．たとえば，一番上だけ見てみましょう．
Grp(H,G1×G2)≅Grp(H,G1)×Grp(H,G2),φ↦(π1∘φ,π2∘φ), という全単射は自然同型である．
次のような関手 F1,F2:Grpop×Grp×Grp→Set を考える： F1(H,G1,G2):=Grp(H,G1×G2),F2(H,G1,G2):=Grp(H,G1)×Grp(H,G2). これらは実際に関手になる．なぜなら，群準同型 φH:H′→H,φ1:G1→G′1,φ2:G2→G′2 を取ったときに，群準同型 F1(φH,φ1,φ2):F1(H,G1,G2)→F1(H′,G′1,G′2) と F2(φH,φ1,φ2):F2(H,G1,G2)→F2(H′,G′1,G′2) が F1(φH,φ1,φ2)(φ):=(φ1×φ2)∘φ∘φH,F2(φH,φ1,φ2)(φ,ψ):=(φ1∘φ∘φH)×(φ2∘ψ∘φH) によって定まるからである．上のように定義される変換を τH,G1,G2:F1(H,G1,G2)→F2(H,G1,G2) とおく．τ:F1→F2 が自然変換であること，すなわち τH′,G′1,G′2∘F1(φH,φ1,φ2)=F2(φH,φ1,φ2)∘τH,G1,G2 を示せばよい．これは定義に従って丁寧に計算すれば確かめられる．